Floating Point Representation

What is Floating Point Representation?

- The term floating point is derived from the fact that there is no fixed number of digits before and after the decimal point; that is, the decimal point can float.

Or We can understand in another way,

Fixed-point number representations has a range that is sufficient for many scientific and engineering calculations. For convenience, we would like to have a binary number representation that can easily accommodate both very large integers and very small fractions. To do this, a computer must be able to represent numbers and operate

on them in such a way that the position of the binary point is variable and is automatically

adjusted as computation proceeds. In this case, the binary point is said to float, and the

numbers are called floating-point numbers.

For Example:

We have to show (6.5)₁₀  in binary number, It'll be (110.1)₂ . As in Scientific Notation,it'll be (1.101 x 2² )₂ .

We conclude that a binary floating-point number can be represented by:

• a sign for the number

• some significant bits

• a signed scale factor exponent for an implied base of 2

Note: When the binary point is placed to the right of the first significant bit, the

number is said to be normalized. [ (110.1)₂ normalized to (1.101 x 2² )₂ ]

In the above Example , (1.101 x 2² )₂  -

It have :

• +ve sign,
• 3 significant bits after decimal i.e., 101,(Mantissa)
• a signed scale factor exponent i.e., 2² .(Exponent)

To store it in computer we use Floating Point Representation:

The IEEE standard specify two types of Floating Point Representation:

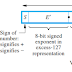
1) Single Precision (32 Bit standard representation)

2) Double Precision (64 bit standard representation)

Note: Instead of the actual signed exponent, E, the value stored in the exponent field is an unsigned integer
 E= E + 127. This is called the excess-127 format. Thus, E is in the range 0 ≤ E ≤ 255.
This means that the actual exponent, E, is in the range −126 ≤ E ≤ 127. The use of the excess-127 representation for exponents simplifies comparison of the relative sizes of two floating-point numbers.
The scale factor has a range of 2⁻¹²⁶ to 2⁺¹²⁷,(approximately 10 E±38). The 24-bit mantissa provides approximately the same precision as a 7-digit decimal value.

Note: The double-precision format has increased exponent and mantissa ranges. The 11-bit excess-1023 exponent E has the range 1 ≤ E ≤ 2046 for normal values, with 0 and 2047 used to indicate special values,
as before. Thus, the actual exponent E is in the range −1022 ≤ E ≤ 1023, providing scale factors of 2⁻¹⁰²² to 2¹⁰²³,(approximately 10 E±308).. The 53-bit mantissa provides a precision equivalent to about 16 decimal digits.


Example of Normalisation (Single Precision):

Example of Single Precision Floating-Point Number:

Here in above example, the exponent (00101000)₂ = 40 and excess-127 is 40-127= -87, (inversely -87+127=40 ).


Note: When E = 0 and the mantissa fraction M is zero, the value 0 is represented. 
When E=  255 and M = 0, the value ∞ is represented, where ∞ is the result of dividing a normal number by zero. The sign bit is still used in these representations, so there are representations for ±0 and ±∞.
When E= 0 and M ≠ 0, denormal numbers are represented. Their value is ±0.M × 2⁻¹²⁶.
When E = 255 and M ≠ 0, the value represented is called Not a Number (NaN). A NaN represents the result of performing an invalid operation such as 0/0 or √−1.


IEEE STANDARDS for Floating-Point Numbers:

	sign	exponent	mantissa	exponent	significant
format	bit	bits	bits	excess	digits
Our 8-bit	1	4	3	7	1
Our 16-bit	1	6	9	31	3
IEEE 32-bit	1	8	23	127	6
IEEE 64-bit	1	11	52	1,023	15
IEEE 128-bit	1	15	112	16,383	34